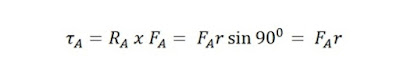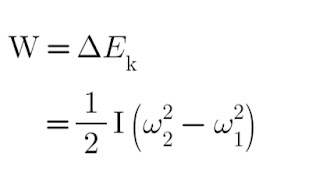Kesetimbangan Benda Tegar
Benda Tegar adalah suatu benda yang jarak antara molekul sembarangan didalamnya adalah tetap.
terdapat dua jenis kesetimbangan benda yaitu kesetimbangan translasi dan kesetimbangan rotasi. Sebelum mempelajari lebih lanjut tentang kesetimbangan, terlebih dahulu kita akan mempelajari satu konsep fisika yang terkait yaitu torsi.
1. Torsi
Jika bekerja sebuah gaya F pada suatu benda di titik dengan vektor posisi r terhadap titik asal, maka pada benda itu bekerja suatu torsi (τ), torsi didefinisikan sebagai F r sin Ɵ, di mana Ɵ adalah sudut yang dibentuk antara vektor F dan r. Kita definisikan torsi sebagai:
τ = r x F
Perhatikan gambar berikut. Dua buah gaya FA dan FB bekerja pada sebuah balok yang memiliki titik berat di O. Jarak AO dan OB adalah r.
Berdasarkan gambar, bekerja dua vektor gaya FA dan FB. Vektor gaya FA bekerja pada A dengan vektor posisi RA = r, sedangkan FB bekerja pada B dengan vektor posisi RB = - r. Perhatikan dengan seksama arah vektor posisi ini.
Gaya FA menghasilkan torsi A (τA) yang berputar searah jarum jam
Gaya FB menghasilkan torsi B (τB) yang berputar berlawanan arah jarum jam
Torsi totalnya adalah
Jika FA = FB maka total torsi adalah nol sehingga tidak terjadi rotasi pada balok.
Contoh Soal:
Dua buah gaya 30 N dan 45 N bekerja pada sebuah benda seperti pada gambar berikut. Diketahui: AB = BC = 50 cm
2. Syarat kesetimbangan benda Tegar
Setelah mempelajari konsep torsi saatnya kita masuk ke dalam konsep kesetimbangan benda Tegar. Sebuah benda dikatakan mengalami kesetimbangan jika memenuhi dua kesetimbangan yaitu kesetimbangan translasi dan kesetimbangan rotasi.
Suatu benda dapat dikatakan setimbang translasi apabila resultan gaya gaya yang bekerja terhadap benda tersebut adalah nol. Jadi syarat kesetimbangan translasi adalah
ƩF =0
Suatu benda dapat dikatakan setimbang rotasi apabila resultan torsi yang bekerja terhadap benda tersebut adalah nol. Jadi syarat kesetimbangan rotasi adalah
Ʃτ = 0
Jika kedua syarat ini terpenuhi pada suatu sistem, maka benda dikatakan mengalami kesetimbangan benda tegar.
3. Hubungan antara torsi dan percepatan anguler
Benda dapat berputar jika bekerja gaya pada benda itu relatif terhadap suatu sumbu putar. Bayangkan saja sebuah pintu. Jika gaya bekerja pada daun pintu, baik gaya tarik maupun gaya dorong, pintu akan bergerak menutup. Berarti ada torsi yang bekerja pada pintu. Akan tetapi, jika gaya dikerahkan pada sumbu putar pintu seberapa pun besarnya, pintu tidak akan berotasi.
Sekarang kita mulai analisis sebuah benda titik yang berotasi pada titik O. Gaya yang menyebabkan adanya torsi pada benda titik sebalik gaya tangensial Ft (gaya tangensial selalu berarah tegak lurus terhadap sumbu putar benda). gaya tangensial ini menyebabkan terjadinya percepatan tangensial at pada objek yang berotasi.
Ft = m at
τ = Ft r
= m at r
Hubungan antara percepatan linier dengan percepatan anguler adalah
a = α r
Maka:
τ = m (α r ) r = m r2 α
Dalam bahasan tentang momen inersia telah kita ketahui
I = m r2
τ = I α
Persamaan diatas, walaupun diturunkan dari benda titik, namun tetap dapat diaplikasikan pada benda-benda Tegar, misalnya, tabung, bola pejal, dan sebagainya. Perlu dipahami bahwa, misalnya pada lempengan logam tipis berbentuk lingkaran yang berotasi, setiap detik mungkin saja memiliki kecepatan dan percepatan linier yang berbeda ( jika jarak titik-titik terhadap sumbu putar berbeda) namun setiap titik pada benda Tegar berotasi dengan kecepatan dan percepatan anguler yang sama.
4. Usaha, Daya, dan Energi pada gerak rotasi
Besarnya usaha dalam gerak rotasi adalah
W = τ Ɵ
Daya P, seperti yang telah dirumuskan sebelumnya adalah usaha persatuan waktu, sehingga:
P = W/t = τ Ɵ/t = τ w
Dimana:
P = Daya (Watt)
τ = torsi
w = kecepatan sudut
Sedangkan energi kinetik linier atau translasi adalah
Ek = 1/2 mv2
Dalam gerak rotasi kecepatan translasi benda adalah
v = w r
Dengan demikian besar nya energi kinetik rotasi adalah
Dalam gerak translasi hubungan antara usaha dan energi kinetik adalah
Sehingga persamaan hubungan antara usaha dan energi kinetik rotasi adalah
5. Rotasi dan translasi pada benda Tegar
Mekanika dalam perspektif benda Tegar yaitu benda yang tersusun atas banyak partikel. bagaimana jika benda Tegar melakukan rotasi dan translasi secara bersamaan?
Maka dapat kita gunakan persamaan di bawah ini:
6. Momentum sudut
Jika sebuah benda memiliki massa m terletak pada posisi r dan bergerak dengan kecepatan V maka momentum sudut benda itu adalah
L = r × p atau L = r mv
Karena: v = wr
Maka:
L = rm (wr)
L= mr2 w
L = I w
Contoh soal:
Sebuah piringan hitam mula-mula berputar dengan kecepatan 20 rad/s. Seorang menambah kecepatan sudut piringan tersebut menjadi 50 rad/s. Diketahui massa piringan tersebut 100 g dan jari-jarinya 20 cm. Hitunglah usaha yang dibutuhkan untuk mengubah kecepatan sudut piringan tersebut.
Diketahui:
w1 = 20 rad/s
w2 = 50 rad/s
m = 100 g = 0,1 Kg
R = 20 cm = 0,2 m
Ditanyakan:
W =...?
Penyelesaian:
I = 1/2 MR2
I = 1/2 0,1 × 0,22 = 0,002 kg m -2
Usaha
W = ∆Ek
W W = 1/2 I (w2 2 - w1 2)
W W = 1/2 × 0,002 × (502 - 202)
W W = 2,1 Joule